x_i^(ℓ) + │ ├───────────┐ │ ( Self-Attention ) │ ┌──────┿──────┐ │ ↓線型変換 ↓ ↓ │ Q_i = x_i W_Q K_i = x_i W_K V_i = x_i W_V │ └──┬───┘ │ │ ↓ │ │ α_i = sim( Q_i ; K_1, ‥‥, K_m ) │ │ │ │ │ └───┬──────┘ │ z_i =α_i V │ │ │← Residual ─────┘ │ │← LayerNorm (正規化) │ ├───────────┐ │ ( FFN ) │ ↓ │ z'_i = σ( x_i W_1 + b_1) W_2 + b2 │ │ │← Residual ─────┘ │ │← LayerNorm ↓ x_i^(ℓ+1) FNN の内容 (計算アルゴリズム) は:
b_1 : dff 次元数ベクトル:第1層のバイアス (bias) b_2 : D 次元数ベクトル:第2層のバイアス z'_i の式は,「多層パーセプトロン (MLP)」の形である。 また,「2層」を見るときは,「2層NN (Neural Network)」である。 diff 通常 dff = 4D 程度 ReLU(Rectified Linear Unit): σ(x) = max(0, x) 負の値を0にし、非線形性を持たせるシンプルな関数。 σ(x) = x⋅Φ(x) (Φ(x) : 標準正規分布の累積分布関数) 滑らかで微分可能 (ReLU の自然な改良版)。 GPTではこちらが主流。 さて,この FFN は,何をしているのか? 2次元数空間 (平面) に,糸と x_i がある様をイメージせよ。 x_i は,移動して糸に乗ることが課題である。 x_i は,,2次元空間の存在なので,糸に対する遠近がわからない。
しかし周りの物を無くなって,片目で対象物を見れば,もう遠近はわからない。 糸の遠近がわからない x_i は,このあなたの場合である。 そこで x_i を,平面が見える3次元の存在にしてやる。 x_i は,糸の真上の位置に移動して,そこから平面に落下する。 これで x_i は糸の上に乗る。 めでたしめでたし。 「z'_i = σ( x_i W_1 + b_1) W_2 + b2」の z'_i は,このときの x_i の移動を表す。 「x_i W_1」は,D次元の存在の x_i を,Dより高次の diff 次元の存在にしてやる。 これにより,x_i は糸が平面に乗っているように見える。 そこで,糸の真上に移動する。──この移動が b_1。 W_2 は「落下」。 b_2 は,落下が糸から外れたときの「補正」。 σ= max(0, x) の意味はよくわからないが,「糸の真上に移動」は何でもありになるので,制限をかけて素直な移動へ導こうということか? 実際 FNN は,Transformer の大部分のパラメータ量を占めるほど,重い処理であるらしい。 よって「自由」をできるだけ抑えることが,重要になる。 Self-Attention と FNN は,どちらも出力が x_i に対する Residual,即ち x_i の移動である。 この2つの移動の違いは? Self-Attention が出力する「移動」は,x_1, ‥‥, x_m のいまの位置関係を大事にした「一斉移動」である。 乗るべき糸へ,全体で移動するというもの。 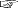 Self-Attention がしていること Self-Attention がしていること
この移動は,全体を大まかに糸に乗せるものである。 よって,糸から外れる個が出てくる。 この個を糸に乗せてやるのが,FFN。 この2段構えは,理に叶っている。 FFN だけだと,せっかく調整が成ったトークン点の布置を,また壊してしまいそうである。 |